1. Searching Ordered Arrays
만약 element가 정렬되어 있지 않다면, linear search($\Theta(n)$)가 가장 최선의 선택지이다.
정렬이 되어 있다면 Binary Search($\Theta(log n)$)이 linear search보다 낫다.
하지만 우리가 사전에 데이터의 분포와 사용 패턴을 알고 있다면 Binary Search보다도 더 좋은 Search Algorithm을 찾을 수 있다.
1-1. Jump Search
k의 범위를 두고, L[0], L[k-1], L[2k-1]...을 순차적으로 방문하며 해당 값이 찾고자 하는 값 K보다 큰지 작은지를 검사한다.
해당 값이 K보다 크다면 계속해서 jump search를 진행하고 아니라면 이전의 값으로 돌아가 Linear search를 시작한다.
Jump search를 위한 최적의 k 값은 얼마인가?
-> 만약 (m-1)k $\gt$ n $\ge$ mk, 라면 jump search의 최종 cost는 m + k - 1이 된더,
Cost T(n, k) = m + k - 1 = $\lceil\frac{n}{k}\rceil$ + k - 1
best k는 그 때문에,
$min_{1 \le k \le n}(\lceil\frac{n}{k}\rceil$ + k - 1)
최적의 k값이 된다.
T'(k) = 0일 때, 최솟값을 가지기 때문에, minimum은 k = $\sqrt{n}$일 때가 된다.
해당 case에서는 T(n, k) = $2\sqrt{n}$의 cost를 가진다.
1-2. Interpolation Search
Dictionary Search라고도 부름 => 사전에서 단어 찾을 때, 맨 첫글자 알파벳부터 찾은 다음 순차적으로 찾아나가는 것처럼 해당 key를 가진 첫번째 index로 접근해 linear search를 시작함.
만약에 sorted array가 주어질 때 해당 접근방법을 사용하면 binary search보다 빠르게 찾을 수 있는가? => 그렇다.

1-3. Quadratic Binary Search(QBS)
Interpolation Search의 variation 중 하나로, p를 계산한 뒤 $L[\lceil pn \rceil]$이 맞는지를 검사한다.
만약 K = $L[\lceil pn \rceil]$라면 종결,
만약 K < $L[\lceil pn \rceil]$라면 해당 지점에서부터 jump search를 수행한다.
K가 해당 지점보다 작아지거나 같아지는 지점까지 jump search를 지속한다.
K > $L[\lceil pn \rceil]$ 일 때도 jump search를 수행
K가 $\sqrt{n}$ 포지션 안에 있다고 가정할 때,
Jump search는 각각 상수 시간복잡도를 가진다고 가정한다.
재귀적으로 해당 process를 이어간다고 가정할 때 cost는 $\Theta(log log n)$으로 계산된다.
(proof)
probe gap은 $sqrt{n}$ -> $sqrt{sqrt{n}}$ -> sqrt{sqrt{sqrt{n}}} -> ...
으로 작아진다. 즉
$n^{1/2}$ -> n^{1/4} -> n^{1/8} -> ...로 줄어든다는 말.
n = $2^{log n}$이기 때문에,
$2^{log n/2}$ -> $2^{log n/4}$-> ... -> $2^1$
즉 시간복잡도는 $\Theta(log log n)$이 된다.
uniformly distributed data의 경우 average number of probes는 2.4이다.
따라서 이를 가지고 Binary Search와 비교하면

큰 n을 가질 때, binary search보다 더 효율적임을 알 수 있다.(total comparison 수의 비교)
사람들은 대부분 자주 검색하는 자료만 검색하기 때문에 앞서 논의한 algorithm보다 더 빠른 algorithm을 설계할 수 있다.
2. Lists Ordered by Frequency
list를 Frequency에 따라 정렬한다.
first record에 접근하는 cost, frequency(확률) : 1, $p_1$
second record에 접근하는 cost, frequency(확률) : 2, $p_2$
라고 할 때,
search cost의 기댓값은
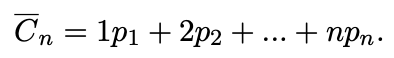
이 된다.
만약 모든 record가 동일한 frequency를 가진다면 해당 비용은

이 된다.
Geometric한 frequency 분포를 가진다면

해당 값을 가진다.(상수만큼 줄어들게 된다.)
80/20의 분포를 가지는 Zipf distribution으로 나뉘어져있다고 한다면
(80%의 access가 20%의 records에만 해당)

대략 0.122n의 비용을 가진다.
3. Self-organizing lists
우리는 사전에 frequency를 예측할 수 없기 때문에, 입력에 따라 data의 order를 바꾸는 self-organizing list를 사용한다.
heurisitc method가 사용되며, 3가지의 접근 방법이 있다.
1) Count
2) Move-to-Front
3) Transpose
3-1. Count Heuristic
각각의 접근마다 count를 해서, Count 값을 기준으로 정렬을 한다.

3-2. Move-to-front Heuristic
해당 값에 대한 search가 있을 때마다 맨 앞으로 위치시킨다.

3-3. Transpose Heuristic
해당 값에 대한 search가 있을 때마다 그 값을 앞에 있는 값과 swap함.

3-4. Text Compression
move-to-front Heuristic을 사용해서 문자메세지에 나오는 단어들을 압축시킨다.
- 만약 단어가 아직 나오지 않았다면 단어 그대로 전송
- 단어가 나왔다면 table에 현재 index 값을 전송시킨 후 move-to-front를 수행한다.


해당 방식으로 바뀌게 된다.
4. Searching in Sets
범위는 작고 찾고자 하는 element가 해당 범위 안에 거의 다 있을 때(dense sets)
사용할 수 있는 기법.
set의 element 하나하나를 bit에 대응시킨다.
logical operator로 set operator를 수행할 수 있다.
예를 들어 0부터 15까지의 수 중에 소수이며, 홀수인 값을 찾고자 한다면

logical operator(&)으로 set intersection을 구해줄 수 있게 된다.
5. Hashing
k가 주어질 때, k를 상수 시간 안에 찾을 수 있는가?
-> Hashing을 사용하면 가능하다.
Hash Table을 사용해서 미리 record를 저장해둔다.(HT은 M개의 slot을 가진다.)
5-1. Hash Function
Hash function은 record(K)에 slot 위치를 배정하는 함수이다.
- 0 $\le$ h(k) $\le$ M - 1
- h(K) = K % M
hashing system의 목적 : hash function을 통해 record를 HT을 배정두고 상수 시간 내에 찾을 수 있게 한다.
Collision : 두개의 다른 key가 같은 slot에 배정받는 것
$h(k_1) = h(k_2) = \beta$
만약 두 개 이상의 record가 같은 slot을 할당 받는 다면 collision resolution policy를 이용한다.
하지만 collision이 일어나지 않는 것이 가장 좋은 hash function이다.!
일반적으로 많이 쓰이는 h(K) = K % 16의 경우 좋은 hash function인가?
(1) even number만 들어올 경우 HT의 50%밖에 사용하지 않는다.
(2) record의 하위 4bit 밖에 사용하지 않아 record의 특성이 무시될 가능성이 있다.
solving (1) -> Use a Prime number for M
M이 7이면, 짝수만 들어오더라도 HT에 골고루 배정할 수 있음.
M과 c가 prime 관계라면,
c * i(i = 0, ,,, M-1)일 때, h(K)는 M개의 다른 slots에 골고루 배정될 것이다.
solving (2) -> 하위 4 bit만 사용한다.
mid-square method를 사용하면 전체 bit를 고려한 hash function을 만들 수 있다.
=> 제곱을 해준 뒤 가운데 r bits를 key 값으로 사용
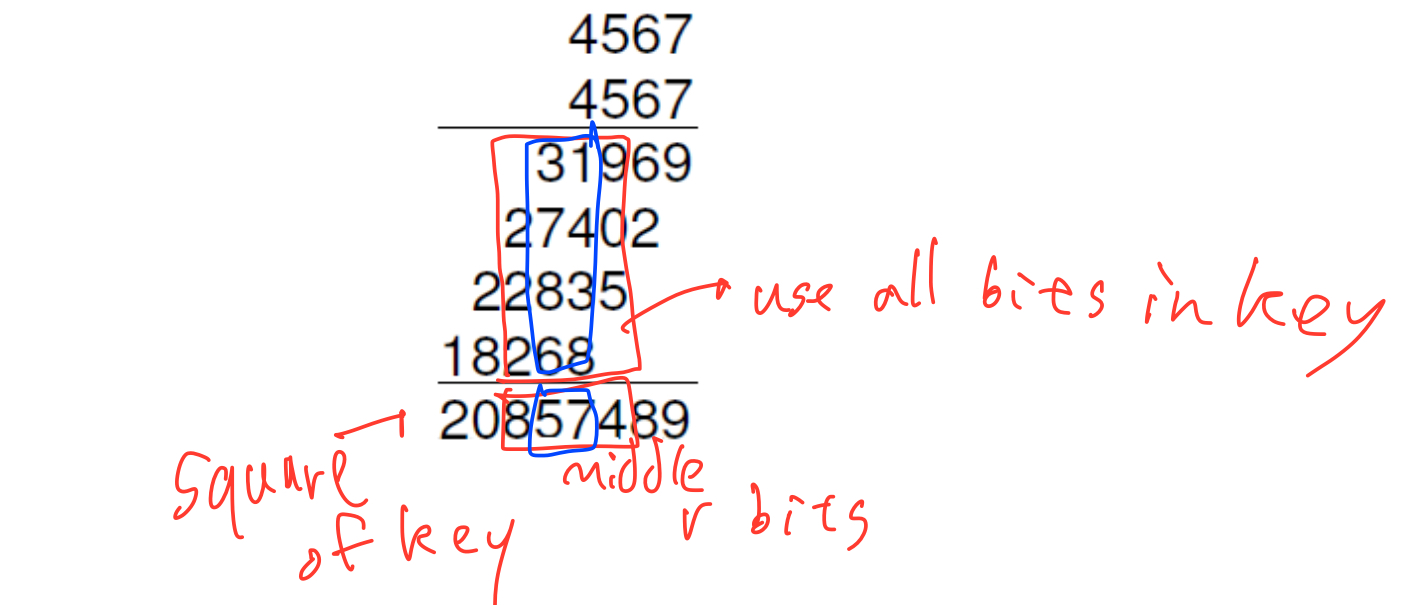
folding approach를 사용하면 수를 byte 단위로 나눠준 뒤 %M을 취해줄 수 있음.

만약 M값이 크고, x의 byte 수가 작을 때,(ex, M = 100001, x = 10bytes) HT의 특정 부분만 사용할 수 있다.

4-byte 단위로 나눠서 더해주면 M 값이 커도 여러 slot에 골고루 할당해줄 수 있다.
5. Collision Resolution
할당되는 HT slot이 같을 때 이를 해결하는 방법
(1) open hashing(separate chaining)
(2) closed hashing(open addressing)
으로 나뉘어진다.
5-1. Open hashing
collision이 발생해도 같은 slot에 해당 record를 저장한다.
Linked list를 이용.
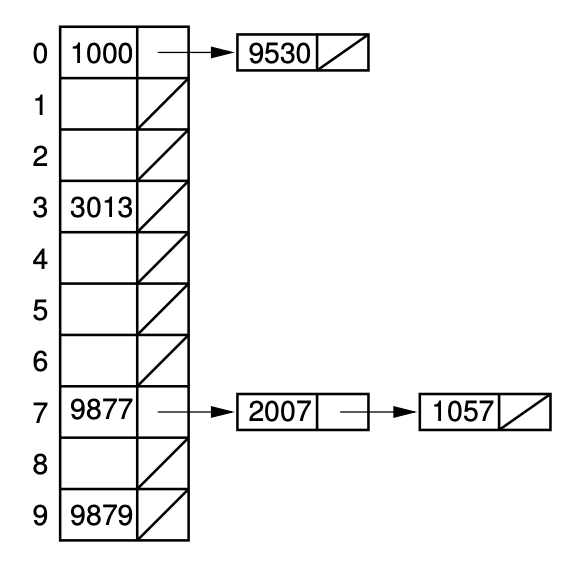
사용되지 않는 HT slot이 생기게 된다.
5-2. Closed hashing
Collision이 일어나면 다른 HT slot에 배정시킨다.
5-2-1. Bucket Hashing

Bucket 단위로 Hash Table을 나누고, Bucket 안에 여러개의 slot을 둬서 가득 찰 경우 다른 slot에 배정되도록 한다.
만약 해당 bucket이 다 찼을 경우에는 Overflow bucket에다 따로 저장한다.
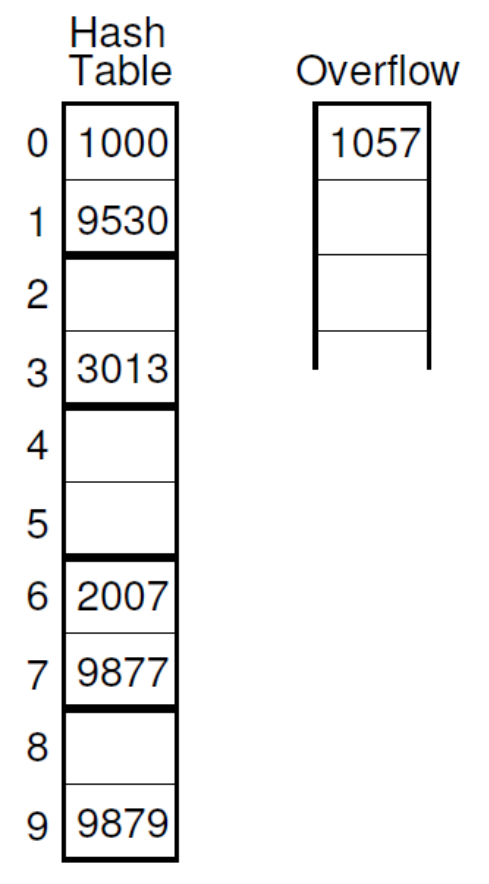
위는 bucket hashing의 variation.
collision이 일어나지 않았을 때는 일반 hashing과 똑같이 사용하다가 해당 slot이 다 찼을 때는 bucket의 다른 slot에다 배정한다.
Bucket hashing vs Open hashing
-> Bucket hashing이 더 많은 collision을 일으킨다. -> key 값이 절반으로 줄어든 것과 같기 때문에,
-> open hashing보다는 더 적은 memory space를 이용한다.
Limitation
-> Bucket이 가득차면 HT에 빈 공간이 남아있어도 overflow bucket 저장한다. -> 메모리 비효율적
5-2-2. Linear Probing
slot에서 collision이 일어날 때 probe_function을 통해 iteration을 거쳐 비어있는 slot을 찾는다.
/* Insert record r with key k into HT */
void hashInsert(Key k, E r){
int home; //Home position for r
int pos = home = h(k); //Initial position
for(int i = 1; HT[pos] != null; i++){
pos = (home + p(k, i)) % M; // Next probe slot
assert HT[pos].key().compareTo(k) != 0 :
"Duplicates not allowed";
}
HT[pos] = new KVpair<Key, E>(k, r); // Insert R
}
Problem of linear probing
: non empty slots이 뭉쳐져있으면, empty slots에 들어갈 확률이 균등하지 않다.
Improved Collision Resolution
- P(K, i) = ci
- c는 M과 소수 관계여야 한다.
- input이 불균등하게 분포되어 있으면 한 section만 많이 쓰이게 된다.
Pseudo-random probing
P(K, i) = Perm[i-1] -> 1과 M-1 의 값 중 random으로 출력
Quadratic probing
-p(K, i) = $c_1i^2 + c_2i + c_3$
5-2-3. Performance of Closed Hashing

점선이 linear probing, 직선이 random proving. -> deletion이 insertion보다 더 적은 cost가 든다.
deletion은 successful search이기 때문.
6. Discussion
probability of collision을 줄이려면 어떤 것이 좋은가?
1. Open hashing - time efficient
2. closed hashing - space efficient
Bucket hashing - small collisions
Linear probing - space efficient
'Computer Science > 자료구조' 카테고리의 다른 글
| Graphs (0) | 2020.12.14 |
|---|---|
| Internal Sorting (0) | 2020.12.13 |
| Non-Binary Tree(General Tree) (0) | 2020.12.12 |
| List, Stacks, and Queues (0) | 2020.10.22 |
| Huffman tree (0) | 2020.10.22 |



