1. General Design Procedure
(1) Understand the problem
=> input과 output은 무엇인가?
(2) Forbulate the problem using a suitable design representation
=> truth table과 waveform을 이용해서 I/O를 가시화'
(3) Choose implementation target
=> ROM, PAL, PLA 등 어떤 게이트를 사용해서 디자인 할 것인가?
(4) Follow implementation procedure
=> K-maps, design tool을 이용해서 implement
ex) BCD to 7-Segment Display Decoder
PLA를 디자인하려는 경우 Product term이 많이 공유되는 것이 좋음

위와 같은 방법으로 겹치는 product term의 개수를 늘려서 unique product term의 개수를 줄임.
PAL에는 겹치는 product-term을 신경쓸 필요가 없다. => OR plane이 이미 고정되어 있음.
2. Case Studies
2-1. Production line control
특정 길이(+-10%)를 가진 rod를 골라내야하는 belt
처음 시작하는 장소 A, 90% 길이인 곳에 B, 110% 길이인 곳에 C 센서를 설치함.
아래와 같은 truth table으로 표현이 가능하다.

2.2 Calendar System
inputs : month, leap year flag
outputs : number of days
Encoding
- binary number for month : 4bits(1~12)
- 하나의 row당 28, 29, 30, 31 중 하나만 1이 된다.
Leap year flag를 결정하는 방식
- Determine value if leaf year flag given the year
=> 4로 나뉘어지지만, 100으로는 나뉘어지지 않고, 그러나 400으로 나뉘어질 때는 괜찮다.
- binary로 encoding하면 4로 나뉘어지는지는 보는게 쉽지만 100, 400으로 나뉘어지는 것을 보기 힘듬
- BCD로 encoding 되어 있으면 100으로 나뉘어지는게 보기 쉬움
Building Parts:
1) construct a circuit that determines if the year is divisible by 4
2) construct a circuit that determines if the year is divisible by 100
3) construct a circuit that determines if the year is divisible by 400
4) 이들을 결합해서 leap year flag를 확인하는 것을 만듬
-BCD를 이용해서 input을 받기로 한다. => 100, 400으로 나누지는 것을 보기 편하도록 하기 위해
leap year flag = D4(D100 * D400)'
= D4 * D100' + D4 * D400
= D4 * D100' + D400
2-3. Telephone Keypad Decoder
1) understand the problem
누른 것을 판별하기 위해서 0과 안누른 상태를 구분하는 것이 필요
Row, Column 별 input을 따로 둬서 해당 번호가 눌렸는지 확인한다.
2) formulate in a standard representation

3) Implementation target
키패드에 눌린 숫자를 4bits로 바꾸는 과정

simultaneous하게 번호가 눌렸는지를 판별

4) Implementation procedure
ROM은 그냥 하면 됨. 번호 K[3:0]과 KP를 나타낼 128 word by 5bit ROM이 필요
PAL은...음,,,어렵다.
2-4. Arithmetic Logic Unit Design
2-5. Combinational Multiplier
3. Arithmetic circuit
- input이 동일하면 무조건 output이 동일하므로 combinational logic에 해당한다.
- time과 space를 trade-off로 가지게 된다. => carry lookahead logic
3-1. integer representations
비트를 숫자로 나타내는 방식
-> 음수를 어떻게 비트로 표현할 것인가가 주된 관심이다.
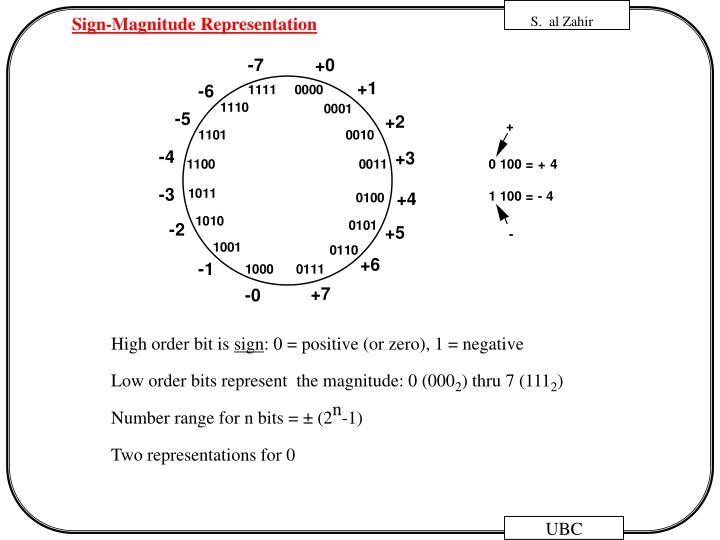
1) sign and magnitude
- MSB가 음수와 양수를 나타내는데 사용된다. 0이면 양수, 1이면 음수
- 나머지 부분이 나타내는 것은 일반 value와 같음
- cumbersome addition/subtraction => 더하기/빼기를 위해 반드시 크기를 비교해주어야 한다.
2) 1s complement
- N이 양수일 때, 음수 N'을 나타내기 위해서 N' = $(2^n - 1) - N$을 계산해준다.
ex) 1s complement of 7
$2^4 = 10000_{(2)}$
$2^4 - 1 = 1111_{(2)}$
$7 = 0111_{(2)}$
$-7 = 1000_{(2)}$
=> 7의 비트를 반대로 바꾸면 -7이 나온다.
=> 여전히 최상위 bit가 sign 판별하는데 사용될 수 있음.
=> 0을 나타내는 비트가 2개이다.

3) 2s complement
- N이 양수일 때, 음수 N'을 나타내기 위해서 N' = $2^n - N$을 계산해준다.
ex) 2s complement of 7
$2^4 = 10000_{(2)}$
$7 = 0111_{(2)}$
$-7 = 1001_{(2)}$
=> 7의 비트를 반대로 바꾼 것에다 1을 더해주면 된다.
=> 최상위 비트가 부호를 판별하는데 사용될 수 있음
=> 0을 나타내는 것이 하나이다.

3-2. addition/substraction
1) 2s complement addition and substraction
-> 가장 쉬운 형태의 더하기와 빼기
-> overflow가 일어나지 않는 범위 내에서는 그대로 연산해도 같은 결과가 나옴.
=> 왜 carry-out을 무시해도 되는가?
-M + N when N > M :
M' + N = $(2^n - M) + N$ = $2^n + (N - M)$
carry-out인 $2^n$은 무시해도 원하는 결과 N-M을 이끌어낼 수 있다.
-M-N when $M+N \le 2^{n-1}$
M* + N* = $(2^n - M) + (2^n - N)$ = $2^n - (M + N) + 2^n$
2^n을 무시하면 우리가 원하는 결과가 나옴
2) sign and magnitude
-> sign이 서로 같을 때는 별다른 것을 고려해주지 않아도 된다.
-> sign이 다를 경우에는 어떤 sign이 나올지 판별한 뒤 계산을 진행해야한다.
3) 1s complement
end-around carry work을 해줘야 한다! => $2^n$을 빼고 1을 더해주는 것과 같기 때문에
M - N = M + N* = $M + (2^n - 1 - N)$ = $(M - N) + 2^n - 1$ (M > N)
-M + (-N) = M* + N* = $(2^n - M - 1) + (2^n - N - 1)$ = $2^n + [2^n - 1 - (M + N)] - 1$
4) Overflow in 2s complement addition/substraction
Overflow가 나는 경우
1) 양수 두개를 더했는데, 음수가 출력되거나
2) 음수 두개를 더했는데, 양수가 출력되는 경우
MSB가 둘 다 0일 때 계산 결과의 MSB가 1이면 overflow
MSB가 둘 다 1일 때 계산 결과의 MSB가 0이면 overflow
3-3. arithmetic/logic units

다음과 같이 게이트 5개로 구현 가능
2) subtractor
adder를 이용해서 subtractor를 구현해줄 수 있다.
A - B = A + (-B) = A + B* + 1
control signal을 통해서 B(adder)일지 B*(subtractor)일지를 선택해줄 수 있다.

3) ripple carry adder
space가 줄어드는 대신 time이 느림
critical delay가 존재

Carry Out이 가장 늦게 계산이 되기 때문에 높은 delay가 생김.
1111 + 0001의 경우 가장 높은 delay가 생기게 된다.
4) Carry-lookahead logic
Carry만 먼저 계산하는 logic
Carry Generator
$G_i = A_i B_i$
=> $G_i$가 1이면 CO는 무조건 1
Carry propagate
$P_i = A_i xor B_i$
=> $P_i$가 0이면 CO는 무조건 0이다.
Sum과 Carry out을 다음과 같이 바꿔줄 수 있다.
$S_i = A_i \ xor \ B_i \ xor \ C_i = P_i \ xor \ C_i$
$C_{i+1} = A_i B_i + A_i C_i + B_i C_i = A_i B_i + C_i(A_i + B_i)$
$= A_iB_i + C_i(A_i \ xor \ B_i)$
$= G_i + C_i P_i$

Carry를 2-level에 계산할 수 있게 된다.
4bits 이상으로 가면 너무 느려지게 됨.

'Computer Science > 논리설계' 카테고리의 다른 글
| Sequential Logic Design (0) | 2020.12.08 |
|---|---|
| Combinational Logic Technology (0) | 2020.10.13 |
| Working with combinational logic (0) | 2020.09.30 |
| Combination logic (0) | 2020.09.15 |
| Introduction (0) | 2020.09.06 |



